





文/李亚洲
公众号/机器之心
机器学习工程师 Adi Chris 最近学习完吴恩达在 Coursera 上的最新课程后,决定写篇博客来记录下自己对这一领域的理解。他建议通过这种方式可以有效地深入理解一个学习主题。除此之外,也希望这篇博客可以帮助到那些有意入坑的朋友。
言归正传。在我正式介绍深度学习是什么东西之前,我想先引入一个简单的例子,借以帮助我们理解为什么需要深度神经网络。

同时,本文附有使用深度神经网络模型求解异或(XOR)问题的代码,发布在 GitHub 上。
GitHub 地址:https://github.com/chrisbangun/medium-post/tree/master/Perceptron-to-DNN
XOR PROBLEM
何为异或问题?对于给定的两个二进制输入,我们通过异或逻辑门得到一个预测输出,这一过程即为异或问题。注意,输入不相等时输出为 1,否则为 0。表 1 展示了异或函数的所有可能的输出结果:

那么现在我们就画出数据分布图来探究它的本质。
def plot_data(data, labels):
"""
argument:
data: np.array containing the input value
labels: 1d numpy array containing the expected label
"""
positives = data[labels == 1, :]
negatives = data[labels == 0, :]
plt.scatter(positives[:, 0], positives[:, 1],
color='red', marker='+', s=200)
plt.scatter(negatives[:, 0], negatives[:, 1],
color='blue', marker='_', s=200)
positives = np.array([[1, 0], [0, 1]])
negatives = np.array([[0, 0], [1, 1]])
data = np.concatenate([positives, negatives])
labels = np.array([1, 1, 0, 0])
plot_data(data, labels)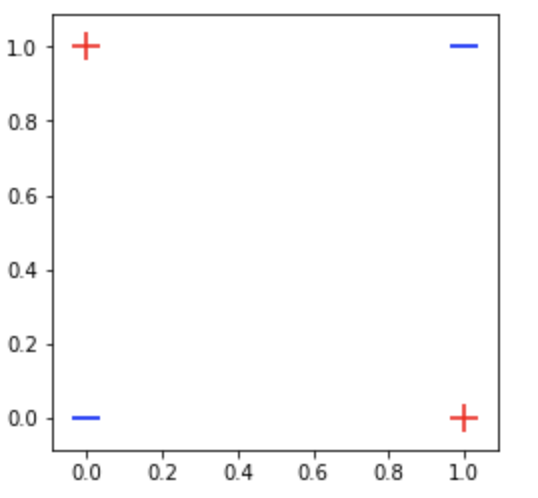
看到上图后,我们或许会反思,这真的是一个简单问题么?
如你所见,我们的数据并非线性可分的,因此,一些常用的线性模型,例如 logistic 回归可能就不太适合分类我们的数据了。为了给你一个更直观的理解,我用一个简单的线性模型画出了如下图的决策边界。
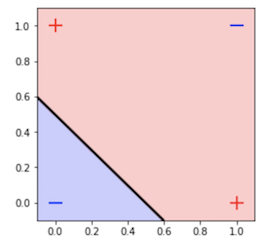
微调 logistic 回归模型构造决策边界
上面的图清楚的告诉我们,我们需要一个更好的分类器来分离非线性数据。SVM 结合它的核心技巧就是一个不错的选择。但是,在本文中,我们打算重新构建一个神经网络而非 SVM,并带你领略下神经网络解决异或问题的风采。
神经网络就是就是找到一个可以模拟人脑工作行为的表现良好的近似函数。图 1 对人类神经元与人工智能网络作了类比。
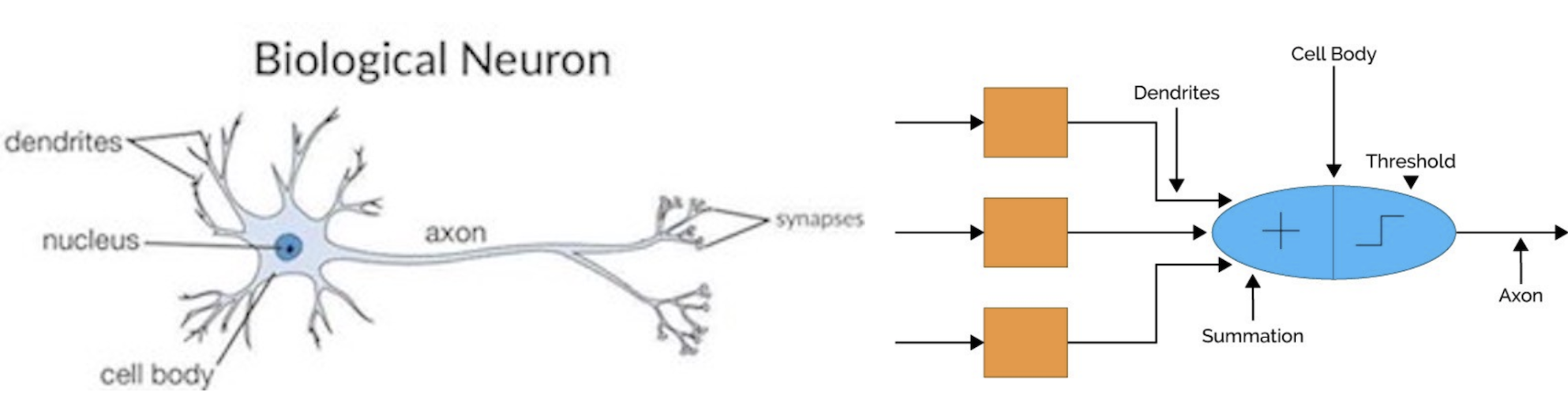
图 1:(a)人脑神经元结构(b)从生理神经网络类比得出的人工智能网络—图片摘自 cs231n.github.io
你不需要了解太多生物学知识,我会从高度形象的角度来解释人体神经元如何处理信息。
人体的神经元通过树突接受信号。这些信息或信号随后被传递到脑细胞或细胞体。在细胞体内部,所有的信息将被加工生成一个输出。当该输出结果达到某一阈值时,神经元就会兴奋,并通过轴突传递信息,然后通过突触传递到其他相连的神经元。神经元间传输的信号量取决于连接的强度。
前面提到的整个流程某种程度上适用于人工智能网络。你可以把树突想象成人工智能网络中基于突触感知器的被赋予了权重的输入。然后,该输入在人工智能网络的『细胞体』中相加。如果得出的输出值大于阈值单元,那么神经元就会『兴奋』,并将输出传递到其它神经元。
这样你就可以理解人工智能网络就是借鉴基本的生物神经元工作原理建模的吧。
为了了解神经网络是如何工作的,我们先来看看一个叫感知机的简单的人工神经网络。
对我而言,感知机是我见过的机器学习中最优雅的算法之一。它于 1950 年代被提出,尽管很简单,但它可以说是很多重要的机器学习算法的起点了,例如 logistic 回归、支持向量机甚至深度神经网络。
那么感知机怎么工作昵?我们以图 2 展开讨论。
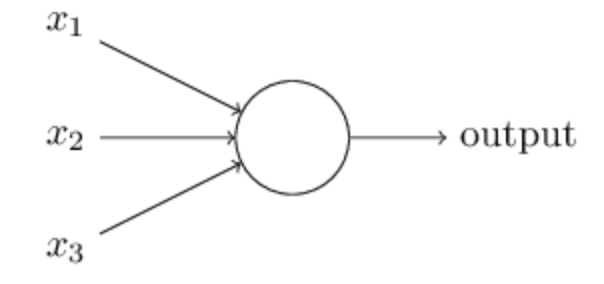
图 2:感知机
图 2 展示了给定三个输入 x_1、x_2 和 x_3 以及一个可以计算输出值的神经元的感知机算法。Rosenblatt 通过引入权重的概念介绍这一简单的规则,用于生成输出值。权重通常是表示输入对应于输出的重要性的实数。上图中的神经元将会得到两个可能的结果,0 或 1,是由每个输入的加权和 ∑wjxj 决定的大于或小于阈值的结果。因此,感知机的主要思想就是去学到一些可以决定神经元兴奋还是抑制的与输入特征相乘的权重 w。我们可以写出一个如下的数学表达式:
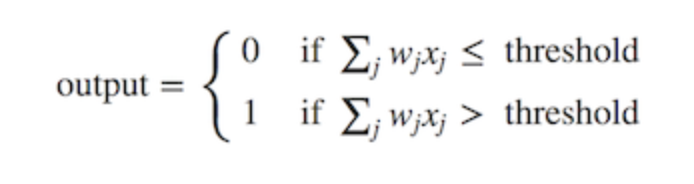
我们现在可以做两件事来修改上述公式:第一,我们把权重相加操作转变成两个向量的点乘。
w (权重) 和 x (输入), 其中 w⋅x ≡ ∑wjxj。接下来,我们可以把阈值移到不等式的另一端并取个新变量名为偏置 b,b 恒等于阈值的负数。通过这些改动,感知机公式重写如下:
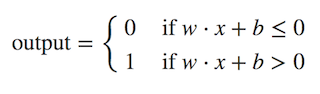
现在我们把这些公式套进我们的感知机架构,这样就有了如下所示的完整的单层感知机架构:
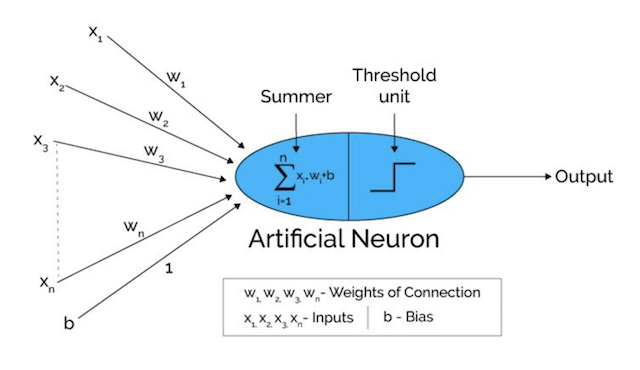
图 3:单层感知机架构
通常情况下,单层感知机模型都会使用阶跃函数作为激活函数将结果转化成 0 或 1,因此将输入归到 0 或 1 类。如图 4 所示,负数的输出为 0,正数的输出为 1。
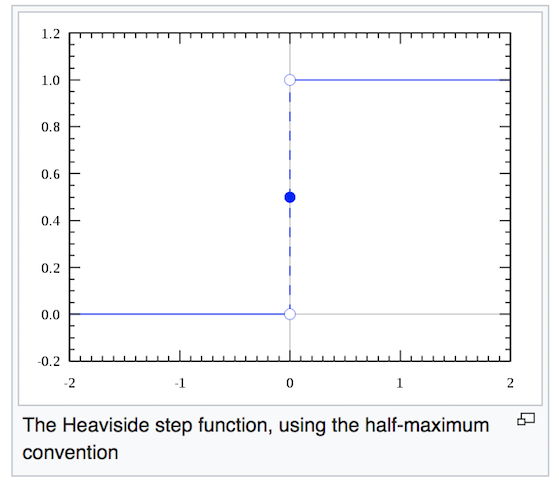
图 4:阶跃函数的图示
对于输入数据线性可分的分类任务,阶跃函数十分有用。但是,由于我们的目的是找到一个用于分离非线性数据的分类器,单层感知机与阶跃函数就毫无意义了。稍后几节,我们将会看到使用非线性激活函数的多层感知机网络模型。
关于我们为什么不用使用阶跃函数,这里有两个主要原因:
1. 目前,结合反向传播使用梯度下降算法是训练一个多层神经网络的有效方法之一(我们稍后会简短的介绍一下)。反向传播的必要条件是使用的激活函数必须可微。然而阶跃函数在 x=0 处不可导,且其它位置导数均为 0。如此一来就无法运用梯度下降法更新权重了。
2. 回想下,神经网络的主要目的就是学习到使预测尽可能接近真实值的权重和偏置。为了达到这一目的,如同很多优化问题,我们希望对权重或偏置上作一个小的改变,在网络输出中只产生一个相对小的变化。而这是一个仅能生成 0 或 1 的函数难以企及的。
激活函数是神经网络的一个重要组成部分。一般来说,我们最少有三个需要激活函数的理由:
我们已经看到以阶跃函数作激活函数的例子,然而,在这一节,我们将要探讨一些深度学习中常用的非线性激活函数。顺便提一下,若要深入了解激活函数,包括每一个激活函数的利弊,你可以参考 Avinash Sharma 和 Karpathy 写的文章。
sigmoid 函数,也即 logistic 函数,对于任意输入,它的输出范围都是 (0,1)。公式如下:

sigmoid 的数学公式
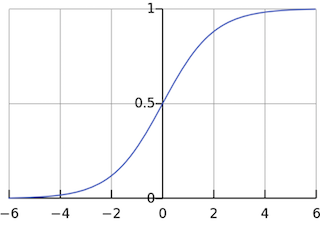
图 5:sigmoid 函数图
图 5 画出了 sigmoid 函数的图形。如你所见,它很像平滑版的阶跃函数。但是,sigmoid 有很多好处,例如:
1. 它是非线性的
2. 不同于二值化输出,sigmoid 可以输入 0 到 1 之间的任意值。对,跟你猜的一样,这可以用来表示概率值。
3. 与 2 相关,sigmoid 的输出值在一个范围内,这意味着它不会输出无穷大的数。
但是,sigmoid 激活函数并不完美:
梯度消失。如上图所示,当输入值 z 趋近负无穷时,sigmoid 函数的输出几乎为 0 . 相反,当输入 z 趋近正无穷时,输出值几乎为 1 . 那么这意味着什么?
在这两个极端情况下,对应的梯度很小,甚至消失了。梯度消失在深度学习中是一个十分重要的问题,我们在深度网络中加了很多层这样的非线性激活函数,这样的话,即使第一层的参数有很大的变化,也不会对输出有太大的影响。换句话讲,就是网络不再学习了,通常训练模型的过程会变得越来越慢,尤其是使用梯度下降算法时。
sigmoid 的另一个弊端就是实际运用中指数运算开销太大。尽管有人说,与矩阵乘法或卷积相比,激活函数在深度网络的计算是非常小的一部分,所以这可能不会成为一个大问题。不过,我认为这值得一提。
Tanh 或双曲正切是另一个深度神经网络中常用的激活函数。类似于 sigmoid 函数,它也将输入转化到良好的输出范围内。具体点说就是对于任意输入,tanh 将会产生一个介于 -1 与 1 之间的值。
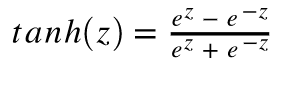
Tanh 函数的数学公式
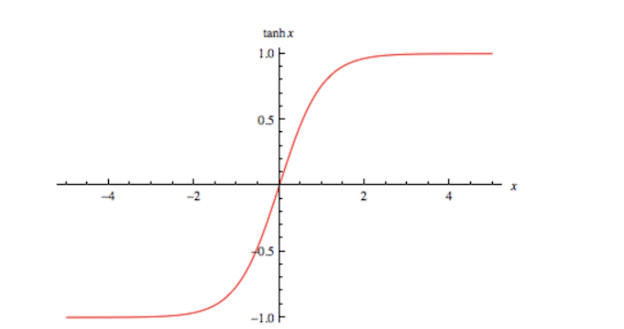
图 6:tanh 函数图
如前面提及的,tanh 激活函数有点像 sigmoid 函数。非线性且输出在某一范围,此处为 (-1, 1)。不必意外,它也有跟 sigmoid 一样的缺点。从数学表达式就可以看出来,它也有梯度消失的问题,以及也需要进行开销巨大的指数运算。
终于讲到了 Relu,人们起初并不觉得它的效果会好过 sigmoid 和 tanh。但是,实战中它确实做到了。事实上,cs231n 课程甚至指出,应该默认使用 Relu 函数。
ReLU 从数学表达式来看,运算十分高效。对于某一输入,当它小于 0 时,输出为 0,否则不变。下面是 ReLU 的函数表达式。
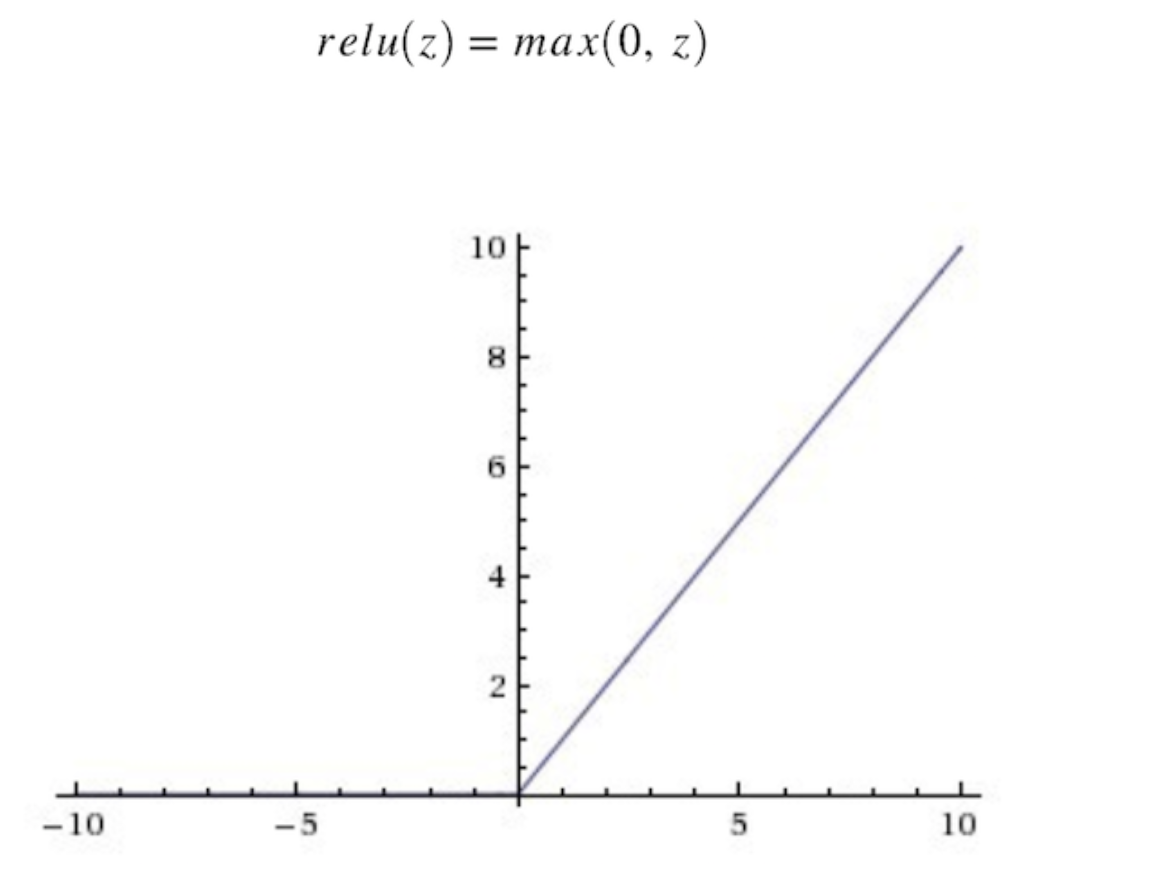
图 7:ReLU 函数图
那么你可能会问,「它是线性函数吧?为何我们说它是非线性函数?」
在线代中,线性函数就是两个向量空间进行向量加和标量乘的映射。
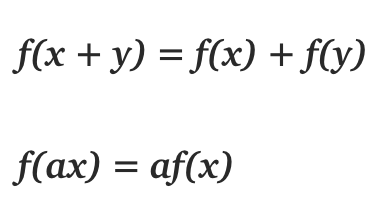
给定上面的定义,我们知道 max(0, x) 是一个分段线性函数。之所以说是分段线性,是因为它在 (−∞, 0] 或 [0,+∞) 上符合线性函数的定义。但是在整个定义域上并不满足线性函数的定义。例如
f(−1) + f(1) ≠f (0)
所以 Relu 就是一个非线性激活函数且有良好的数学性质,并且比 sigmoid 和 tanh 都运算得快。除此以外,Relu 还因避免了梯度消失问题而闻名。然而,ReLU 有一个致命缺点,叫「ReLU 坏死」。ReLu 坏死是指网络中的神经元由于无法在正向传播中起作用而永久死亡的现象。
更确切地说,当神经元在向前传递中激活函数输出为零时,就会出现这个问题,导致它的权值将得到零梯度。因此,当我们进行反向传播时,神经元的权重将永远不会被更新,而特定的神经元将永远不会被激活。
还有件事值得一提。你可能注意到,不像 sigmoid 和 tanh,Relu 并未限定输出范围。这通常会成为一个很大的问题,它可能在另一个深度学习模型如递归神经网络(RNN)中成为麻烦。具体而言,由 ReLU 生成的无界值可能使 RNN 内的计算在没有合理的权重的情况下发生数值爆炸。因此反向传播期间权重在错误方向上的轻微变化都会在正向传递过程中显著放大激活值,如此一来学习过程可能就非常不稳定。我会尝试在下一篇博客文章中详细介绍这一点。

图 8:多层感知机
图 8 所示架构叫多层感知机(MLP)。从名字我们就可以推知,我们只是简单地堆积多层感知机而已。上图是一个三层感知机模型:一个输入层、一个隐藏层,以及一个输出层。然而,在深度学习或神经网络领域,人们并不叫它三层神经网络。通常,我们只统计隐藏层或其加上输出层的层数,因此,上图的网络也叫两层神经网络。隐藏层并不单单指输入层或输出层。现在,如你所猜,所谓的深度学习,就意味着有更多的隐藏层。
那么神经网络如何进行预测昵?
当所有的输入通过所有隐藏层到输出层后,神经网络就会产生一个预测。这一过程叫前馈。如图 8 所示,网络接受输入 X,然后计算激活函数并逐层传递,直到输出。在监督任务中,对于此类分类任务,我们通常在输出层使用一个 sigmoid 函数,以便将预测值转化为概率值。在图 8 中,我们可以看到输出值为 0.24,由于它小于 0.5,我们可以说预测值 y_hat 为 0 .
跟一般的分类任务一样,我们有一个代价函数,用于评估我们的模型拟合真实标签的程度。事实上,训练神经网络可以简单地看作尽可能最小化代价函数的过程。我们可以定义如下的代价函数:
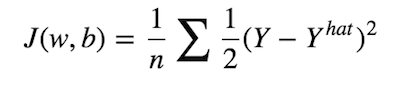
均方误差
所以我们的目的就是找到最佳 w 和 b,使代价函数 J 尽可能的小。为了达到这一目的,我们得靠两大重要的算法,梯度下降和反向传播。
对那些已经接触过机器学习的人来说,你们已经很熟悉梯度下降法了。训练神经网络与训练任何其它使用梯度下降法的机器学习模型没有多大区别。唯一明显的区别是网络中的非线性效应使得我们的代价函数非凸。
为了帮助你理解,我们假设有一个如下图 9 所示的凸代价函数:
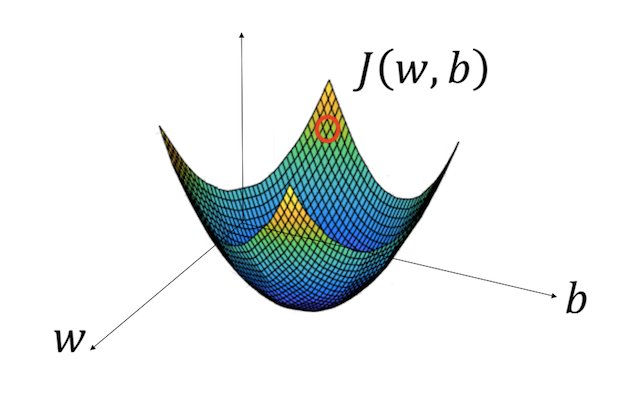
图 9:梯度下降法图解
上表中,水平坐标表示参数空间,权重和偏置,代价函数 J(w, b) 就是水平轴上面的抛物面。图中的红色圆圈代表初始权重 w 和 b 对应的代价。为了最小化这一代价,我们需要走到这个抛物面底。那么问题来了,我们怎么知道沿哪个方向走昵?是参数变大的方向还是变小的方向?我们可以做一个随机搜索,但这显然耗时且开销过大。
通过处理可学习的权重和偏置可以找到最佳方向。微积分告诉我们,在给定的点上,梯度方向就会指向函数值改变最快的方向。因此,我们将使用代价函数对权重和偏置的梯度。
现在,我们简单地看看图 10 所示的代价-权重变化。
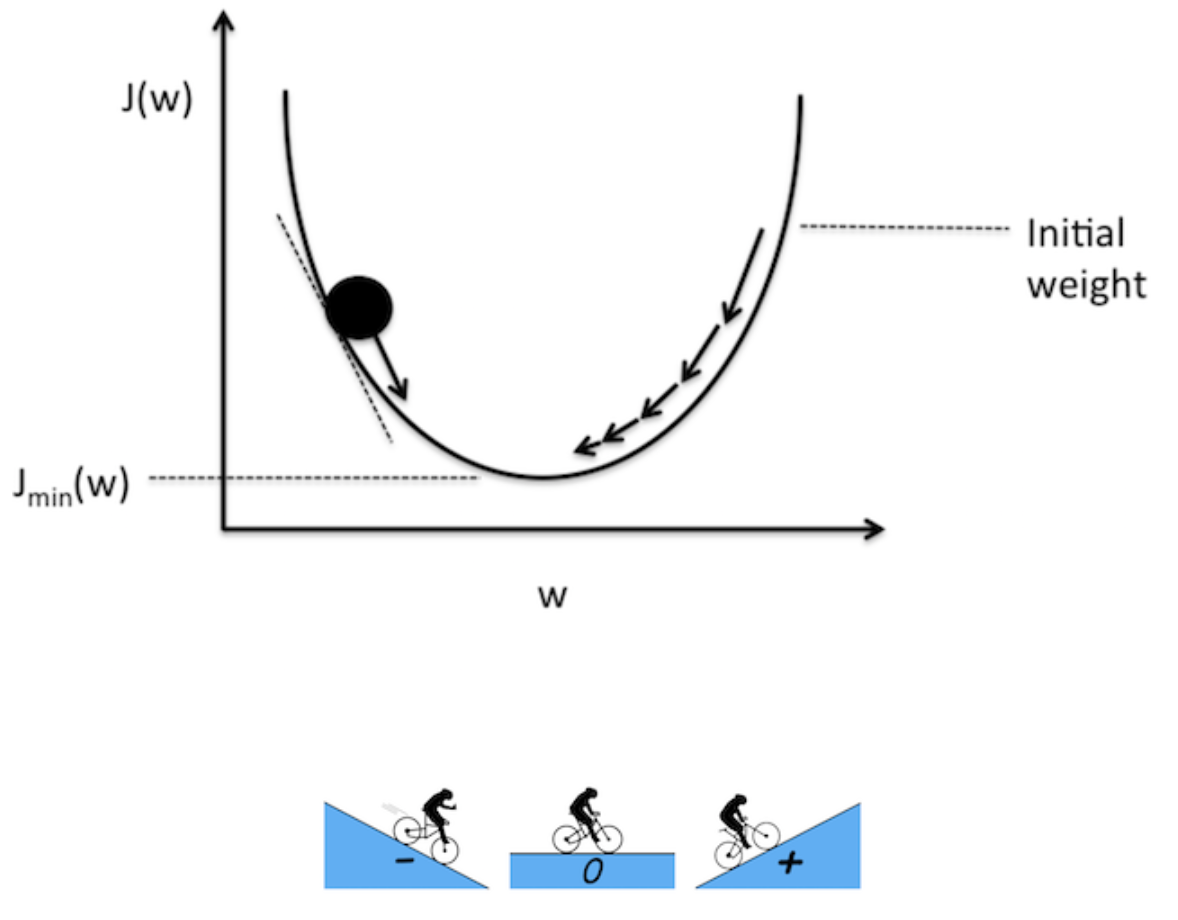
图 10:梯度的形象化表示
图 10 描绘了代价函数对应权重的函数值。你可以把图上的黑色圆看作初始代价。考虑到函数或变量的梯度可负可正可 0。负梯度意味着该线反向倾斜,反之亦然。现在,我们的目的是最小化代价函数,我们就必须沿着梯度的反方向更新权重。这一更新过程可以用以下公式表示:
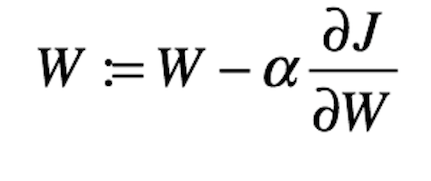
图 11:梯度下降法的参数更新
其中α是步长或学习率,我们将它与可学习参数 w 的偏微分相乘。所以α有啥用昵?
梯度告诉我们哪个方向函数值改变的最快,但是它并未告诉我们应该沿这一方向跨多大步。我们需要一个超参数去控制步长的大小,例如,我们沿某一方向该移动多远,这就是 α 存在的意义。选取正确的学习率十分重要,因为它对两方面有很大的影响:算法的学习速度和我们是否收敛到局部极小值。实际运用中,你可能会运用一个自适应学习率算法,例如动量算法、RMSProp、Adam 等等。AYLIEN 的一个大佬写了一篇关于学习率算法的很棒的文章(如下参考第一篇)。
我们在前一节讲述了梯度下降算法,它是深度学习的学习问题的一个优化算法。考虑到我们需要计算关于可学习参数 w 和 b 的偏微分才能使用梯度下降法。换句话说,我们需要计算 w 和 b 的偏微分。
但是,如果我们仔细看看代价函数 J,下图 12 所示,就会发现 J 和 w 、 b 并没有直接关系。
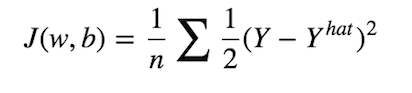
图 12:均方误差
只有从得到 y_hat 的输出层追溯到输入层,我们才会发现 J 与 w 、b 的间接关系,如下图 13 所示:
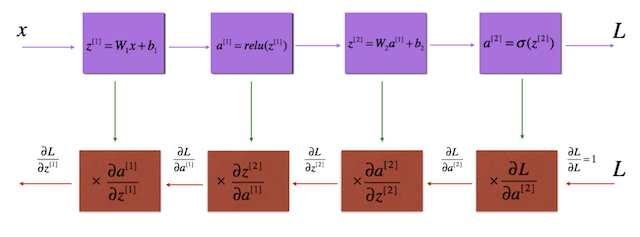
图 13:反向传播图解
你现在应该明白,为了得到代价函数的参数关于 w 和 b 的梯度,我们需要计算所有参数的偏微分,例如前面层的*a* (激活函数) 和 *z* (线性运算: wx + b),这就是反向传播存在的意义。反向传播其实就是反复运用微积分的链式法则,这可能是神经网络中最有效的计算可学习参数梯度的方法了。
接下来,我手把手带你算一下代价函数对第二层神经网络权重 w2 的梯度,简单起见,我们使用图 8 的结构,一个包含三个神经元的隐藏层。
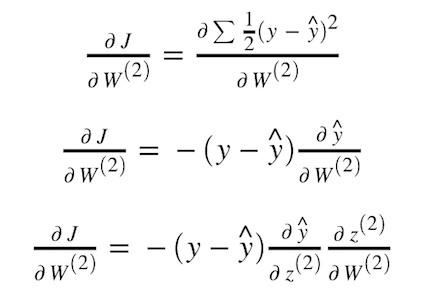
为了得到 y_hat 对 z2 的变化率,我们需要对 sigmoid 激活函数的 z 求微分。
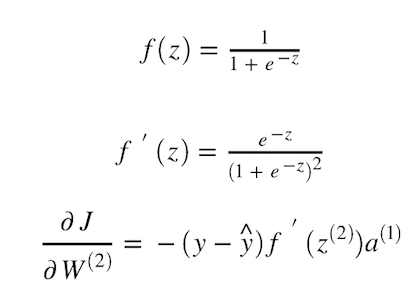
一旦我们得到 J 对 W2 的偏导值,就可以使用图 11 中的公式更新 W2 的值。
我们通常对所有可学习参数重复这一过程,直到得到尽可能小的代价函数值。
不错!我想我们已经了解了如何构建一个神经网络模型甚至深度学习模型的所有知识,这些知识将帮助我们解决异或问题。
写这篇博客时,我顺便搭了一个简单的单隐藏层神经网络模型。图 14 是我使用的样例网络。我画出了一些由我的模型生成的不同数量的神经元的决策边界。如你后面将看到的,包含更多的神经元会使网络模型变得更加复杂,从而创造一个更复杂的决策边界。
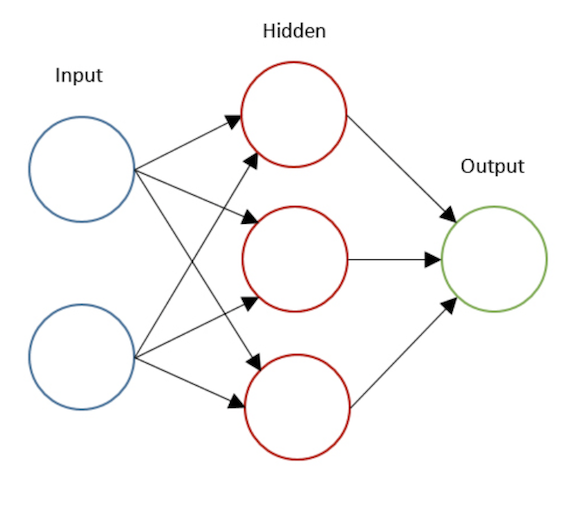
图 14:3 隐藏神经元的两层神经网络
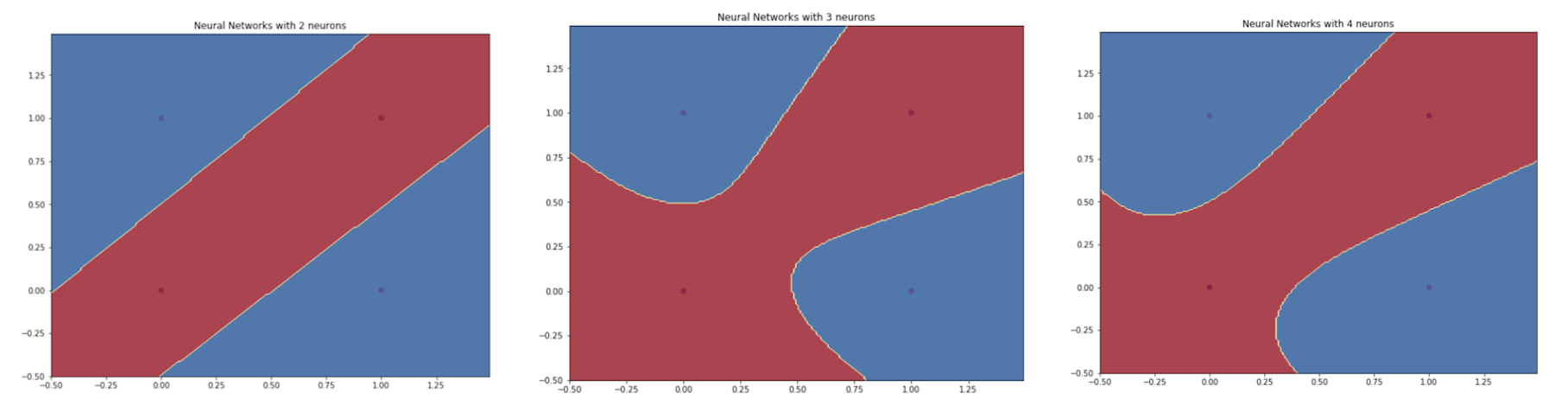
图 15:由一个包含多个神经元(2 个、3 个、4 个)的隐藏层生成的决策边界
但是,到底怎样才是最佳选择?包含更多的神经元还是更多的隐藏层?
理论上讲,网络深的主要好处就是可以表示更复杂的函数。具体而言,通过使用更深层次的网络结构,我们可以学习许多不同抽象层次的特征,例如,从边缘(较底层)到非常复杂的特征(较深层)。
然而,实际中使用深度网络并非总是有用。我们训练深度网络时最常遇到的就是梯度消失问题:一个非常深的网络通常会发生某个梯度迅速变为零的状况,因此使得梯度下降非常缓慢。
再具体点说,使用梯度下降时,因为反向传播是从输出层传播到输入层,而从输入到输出的每一步都是权重矩阵的相乘,因此梯度可能呈指数衰减到 0,某些情况下甚至会发生梯度爆炸。
为了结束这篇冗长的博文,简要总结的要点如下: